About the design
Marjoree is a highly versatile sans serif type family with a distinctive contemporary aesthetic. Designed as a duplex font, Marjoree can switch between weights without any reflow of the text. Marjoree offers clear legibility in small sizes and shows great character and detail in large headlines. These features make Marjoree a practical typesetting tool: In book design, where small changes to the weight can have a big impact across many pages; and in web design, where variable font animations expand creative opportunities.
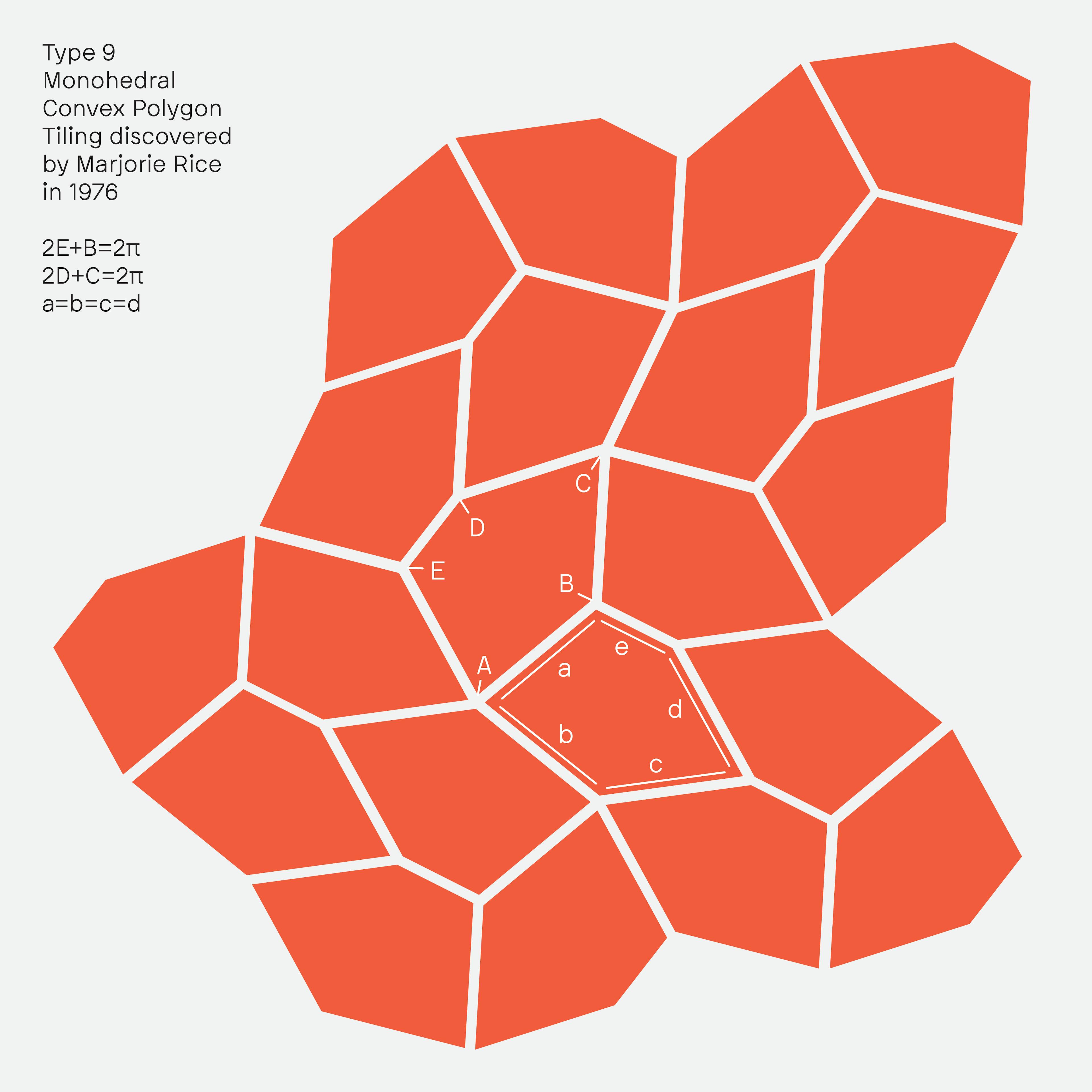
The typeface is named after Marjorie Rice, an amateur mathematician, who did invaluable work on pentagonal tessellations. Between 1975 and 1977 she discovered four new types of tessellating pentagons and developed a notation method to describe them.
In addition to classic Monospace and Proportional styles, Marjoree comes with two experimental titling styles that celebrate their mathematical heritage and push the edges of the variable font format. Based on modular tessellations, Marjoree Hexagon and Marjoree Pentagon have the capability to transition seamlessly between positive type and inverted type. Blurring the boundaries between typography and pattern, Marjoree Hexagon and Pentagon invite to experiment, animate and explore.